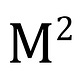Where Trump And Biden's Supporters Walk Off A Cliff Together
2+2=4 but so does 2*2.
Two plus two equals two times two. I learned at an early age why this is important. When I was in algebra I realized a mathematical hack is to simply plug numbers into an equation to solve it using brute force. Also, this is a good technique to check one's work. To verify that
is equal to
simply plug into each equation numbers for x & y using the same x and same y in both equations to see if each yields the same result. For example if x = 3 and y = 5, then in both equations the answer is 5,168. A fairly good check that the two equations are equivalent.
But beware, do not use the number 2 (or -2 when dealing with exponents) for both variables. Why? Because 2 + 2 = 2 * 2. You may get a spurious result simply because of this relationship.
For example
is equal to
IFF x & y both equal 2 or -2 or any number from the set {1, -1, 0}. For any other whole number combinations the answers are different; therefore, the equations are not equivalent.1
In the simplest case (x+y)=(x*y) only when x & y both equal 2, 1, or 0.
There is another lesson to be learned from the 2 + 2 = 2 * 2 relationship. If that is all you ever heard about addition and multiplication, you might mistakenly think the two are equivalent—that addition and multiplication always have the same result.
This is where supporters of Trump and Biden, et al. come in. I am calling out the supporters of these criminals rather than the criminals themselves because I'm not sure these men and all the other politicians like them actually fall for the bad reasoning I'm calling out. Rather I think they prey upon those who are themselves subject to it.
How do the supporters think that addition = multiplication? By not understanding how free trade and free migration actually work.
When I buy something from someone or some firm in China, they get my dollars (suppose $50) and I get the thing I’m buying (say, a pair of shoes). We both thought at the time of the exchange this was a good deal for each of us. Already we see an example of multiplication where addition might be mistakenly assumed.
Specifically, it looks to the naïve observer that I have simply reduced my personal balance sheet by $50 and increased it by a pair of shoes “worth” $50. The reverse is the case for the seller from China. I don’t know about you, but I don’t spend much time trying to make even swaps. Rather I look for bargains. Hence, I bought the shoes because I would rather have the shoes than have the $50. So to me the shoes are “worth” some amount more than $50.2
So immediately the seller and I have multiplied our wellbeing to be some amount greater than $100 rather than simply added it up together for a sum of $100, which it was before the trade occurred. But it gets better . . .
The seller from China now has something that in its current form she probably doesn’t want—50 USD. She would rather have Renminbi.3 To get them she either trades the dollars straight up for some amount of Yuan or she buys something from someone who will take dollars or she invests (again buying) some asset that can be purchased in dollars. Although she is a motivated seller, she still is hunting for a bargain. Hence, she is looking for something she’d rather have than the 50 USD. So again, some multiplication occurs.
Does it matter where the seller is from, in this case China? Wouldn’t the same be true if the seller was from Iowa—a domestic transaction? Yes, indeed the analysis and resulting implication would be the same. However, it does matter in that by growing the market beyond the borders of the USA we multiply the gains. Someone who confuses addition and multiplication wouldn’t realize this, though.
To that naïve observer it looks like we simply have swapped out a USA seller and swapped in a China seller. The USA seller’s loss is the China seller’s gain and the USA buyer is left the same. Not so by a long shot.
Have you ever chosen to shop at a new store? Have you ever eaten at a new restaurant? In these cases I mean “new” as newly open rather than just new to you. For example, a new store comes to town, and you go there repeatedly to buy stuff you previously always have purchased at an old store in town. What has happened? You have benefited over and above the gain you believed you were achieving in the prior buyer/seller arrangement. Otherwise, why would you make the change? The new seller benefits and the old seller suffers (yes, there is a cost to progress). I’ll leave for another day why the new seller’s gain on average in the long run must at least equal if not exceed the old seller’s loss, but suffice it to say we know this because otherwise we would have a shrinking economy—an unsustainable trend.4
Adding people and firms from China to the accessible market of potential buyers and sellers is a multiplication of the market and its benefits. Another way to see this is with a stylized numerical example of possible individual transactions.
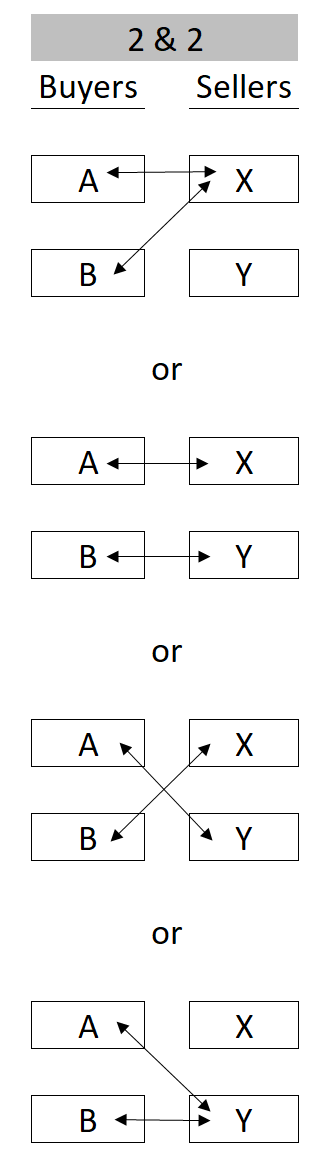
If there are 2 buyers (A & B) and 2 sellers (X & Y) in the USA, there are 4 possible arrangements:
What happens if we add a seller (from China perhaps) to the mix? Well, we don’t just add possible outcomes. If there are still 2 buyers (A & B) but now 3 sellers (X, Y, & Z), there are 9 possible arrangements:
We added 1 and multiplied by 2.25!
If there are 3 buyers (A, B, & C) and 3 sellers (X, Y, & Z), there are 27 possible arrangements! The addition of buyers or sellers multiplies the possible outcomes and, hence, multiplies the potential gains from trade.5
These effects are even more pronounced when it comes to immigration because in that case we are adding both buyers and sellers to the market at the same time. It is equivalent to the growth in the buyer/seller market from the 2 & 2 world to the 3 & 3 world.
Fortunately we live in a world of multiplication. Unfortunately too many of us wrongly believe we are limited to addition.
This problem can also occur in certain circumstances when the same number is used for both x & y. It is just more prevalent in cases where 2 & 2 are used. And it should be even more obvious why 1, -1, and 0 would be bad choices.
“But everyone has to have shoes! That’s a horrible example. In most cases just like this we are simply buying things we have to have for whatever the [greedy companies] make us pay.” I hear some object.
Well, let me be frank: If you think you go about buying things at only the price at which they are worth to you, that you are totally indifferent between the things you buy and the money you give up for it, I REALLY, REALLY want to do some trading with you. Please bring me all your stuff, and I’ll bring my money.
Pedantic note: the Chinese currency is called Yuan Renminbi or Renminbi while the unit of account, number if you will, is Yuan. In the US we use the same term for each, “Dollar”. Think about it this way, “That [Chinese billionaire] has a lot of Renminbi. I think it is about 9,500 billion Yuan.”
“That’s exactly what we have, you fool!” I hear some shout. We are about 250 years down the supposed road to ruin, and there is no sign of it happening yet. But sure, keep screaming about that falling sky.
The equation is # of sellers (3) raised to the # of buyers (2). Alternatively, it can be stated as the number of options for buyer A (3) multiplied by the number of options for buyer B (3). I imposed a limiting assumption in this example that buyers are only purchasing once such that a seller can have multiple buyers but once a buyer makes a purchase, he will not make another. Reversing it would yield the same number of combinations, and the picture would look reversed. Allowing multiple iterations of buying and selling would be more complicated, more realistic, and an even greater demonstration that multiplication rather than addition governs.